Расчет полного сопротивления движению судна путем пересчёта коэффициента сопротивления движению
Приближённое определение сопротивления по прототипу основано на использовании полученной в результате модельных испытаний зависимости коэффициента остаточного сопротивления ![]() , для судна с формой обводов, аналогичной принятой для рассчитываемого объекта, и по возможности с небольшими различиями в основных геометрических характеристиках корпуса. При этом влияние на остаточное сопротивление несоответствия геометрических параметров, как правило, соотношений главных размерений
, для судна с формой обводов, аналогичной принятой для рассчитываемого объекта, и по возможности с небольшими различиями в основных геометрических характеристиках корпуса. При этом влияние на остаточное сопротивление несоответствия геометрических параметров, как правило, соотношений главных размерений ![]() ,
, ![]() ,
, ![]() , коэффициентов полноты
, коэффициентов полноты ![]() ,
, ![]() , а иногда и абсциссы центра величины
, а иногда и абсциссы центра величины ![]() учитывается введением системы корректирующих поправок в исходные значения
учитывается введением системы корректирующих поправок в исходные значения ![]() для прототипа. Применение указанных поправок основывается на допущении о независимости влияния на остаточное сопротивление каждого геометрического параметра из числа различающихся у проектируемого судна и прототипа, при этом остальные параметры полагаются постоянными.
для прототипа. Применение указанных поправок основывается на допущении о независимости влияния на остаточное сопротивление каждого геометрического параметра из числа различающихся у проектируемого судна и прототипа, при этом остальные параметры полагаются постоянными.
Кроме использования для расчёта коэффициента ![]() по прототипу непосредственно материалов систематических серий, существуют комплекты графиков, построенных специально для определения «коэффициентов влияния». Наиболее известные из них диаграммы, построенные И.В. Гирсом, учитывающие влияние относительной длины
по прототипу непосредственно материалов систематических серий, существуют комплекты графиков, построенных специально для определения «коэффициентов влияния». Наиболее известные из них диаграммы, построенные И.В. Гирсом, учитывающие влияние относительной длины ![]() y, коэффициента продольной полноты
y, коэффициента продольной полноты 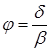 и отношения ширины к осадке
и отношения ширины к осадке ![]() . Именно этими диаграммами мы и будем пользоваться в наших расчётах.
. Именно этими диаграммами мы и будем пользоваться в наших расчётах.
Рассчитаем полное сопротивление движению судна по данным прототипа для полной осадки (таб. 5.1) и построим графическую зависимость ![]() .
.
судно гребной винт лопасть
Таблица 5.1
Расчёт буксировочных сопротивления и мощности путём пересчёта коэффициента остаточного сопротивления по прототипу
|
№ |
Обозначение расчётных величин |
Численные значения | ||||
|
1 |
|
5,000 |
10,000 |
15,000 |
20,000 |
25,000 |
|
2 |
|
2,570 |
5,140 |
7,710 |
10,280 |
12,850 |
|
3 |
|
6,600 |
26,420 |
59,440 |
105,680 |
165,120 |
|
4 |
|
0,060 |
0,110 |
0,170 |
0,220 |
0,280 |
|
5 |
|
0,650 |
0,700 |
0,720 |
1,000 |
1,050 |
|
6 |
|
1,080 |
1,075 |
1,074 |
1,067 |
1,059 |
|
7 |
|
0,920 |
0,950 |
0,940 |
0,920 |
1,070 |
|
8 |
|
0,970 |
0,970 |
0,970 |
0,970 |
0,970 |
|
9 |
|
0,630 |
0,690 |
0,710 |
0,950 |
1,150 |
|
10 |
|
3,097 |
6,194 |
9,290 |
12,387 |
15,484 |
|
11 |
|
1,827 |
1,673 |
1,585 |
1,532 |
1,500 |
|
12 |
|
0,200 |
0,200 |
0,200 |
0,200 |
0,200 |
|
13 |
|
0,100 |
0,100 |
0,100 |
0,100 |
0,100 |
|
14 |
|
2,757 |
2,663 |
2,595 |
2,782 |
2,950 |
|
15 |
|
51,495 |
199,109 |
436,518 |
832,025 |
1378,504 |
|
16 |
|
132,343 |
1023,419 |
3365,557 |
8553,217 |
17713,781 |
|
| ||||||
Информация по теме:
Анализ производительности и фонда оплаты труда
Следует произвести пофакторный анализ выполнения плана по производительности труда. Расчеты целесообразно произвести в табл. 6.1. Расчет данных для таблицы 6.1. ведется в следующем порядке: 1. На основе данных приложения 1 определим численность независящего (условно-постоянного) контингента: =14550 ...
Общие положения по охране труда
Основные понятия в области безопасности труда социальная направленность охраны труда. Под охраной труда понимают систему законодательных актов и соответствующих им мероприятий, направленных на сохранение здоровья и работоспособности трудящихся. Система организационных и технических мероприятий и ср ...
Характеристика микрорайона Защита
Микрорайон Защита располагается в восточной части города. Улично-дорожная сеть района включает в себя несколько основных улиц городского значения. Это улицы Грейдерная, Лениногорская. Планировочная структура поселка преимущественно прямоугольная. В этом районе распложена железнодорожная станция «ЗА ...
Навигация
- Главная
- Транспортная логистика
- Основные понятия грузоведения
- Строительство автомобильных дорог
- Обслуживание локомотивов
- Автомобильный транспорт
- Моторные масла
- Материалы

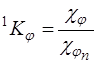 , где
, где 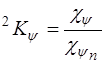 , где
, где  , где
, где 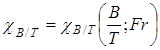 и
и 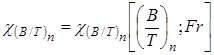 рис 1.69 [1];
рис 1.69 [1];